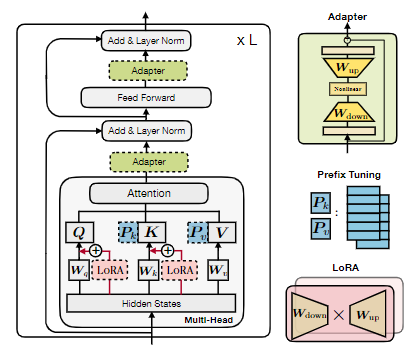
今年以来,在模型越来越大、计算资源越来越紧张的背景下,低参数的微调方法(parameter-efficient fine-tune)越来越受到关注。其中代表性的方法有:LoRA、Prefix-tuning、P-tuning、Adapter。一方面,PEFT 能够节省一定的计算显存和时间,另一方面,在单一任务或垂直领域上,也能够获得和全参数微调可比的性能。
本文从统一视角出发,探讨了几种方法及其优劣和可能的扩展算法。采用统一视角的好处是,可以发现这些单独提出的方法的不足,并获得组合或衍生方法。工程上,也方便在预训练框架中抽象出来,以较高扩展性的方式实现一系列微调方法。
低参数微调的本质是找到一个在特定领域内的等价低维参数优化空间。全参数微调影响的是整个层间输出的隐层状态 h,而低参数微调则是学习隐层状态的增量 Δh,因此也称为 delta tuning。因此,我们可以从一个泛化的统一视角看待,现有的高效微调方法则是一些特例,有这样几个设计维度值得考虑。
Function 如何降维计算增量
$$ \Delta ℎ=f(x,ℎ,(W_{down1},...)) $$
Modification 影响哪一层的 ℎ
Insertion 并行还是串行地计算 ℎ 和 Δℎ
Composition 如何计算 ℎ′=f (ℎ,Δℎ)

LoRA(Low-rank Adaption)[2]基于LLM的低秩假设:预训练的语言模型具有较低的“内在维度”,即使在随机投影到更小的子空间时,它们仍然可以有效地学习。LoRA选择以简单的加性形式修改注意力层的输出。非线性降维采用了proj down → nonlinear → proj up结构:
$$ \Delta h =\Delta W x =W_{up} ( W_{down} x ) $$
可以看到这个模块只与每一层的输入有关,与 ℎ 无关,因此可以并行计算。这也意味着它可以在推理时与主网络合并。
需要注意的是,LoRA 并没有减少计算 ℎ 的计算量,而是节省了 optimizer 所占用的显存。由于 optimizer 中更新参数的数量减少到了仅仅两个矩阵:
$$ W_{down} \in \mathbb{R} ^ {d \times r}, W_{up} \in \mathbb{R} ^ {r \times d} $$
因此,可以减少存储其他 optimizer 状态的空间。此外,LoRA 运算速度更快,也可以减少通信量。
Adapter 往往在不改变模型主干结构情况下,接不同的输出层以适应不同任务。组合函数 同样是加性形式 ℎ′=ℎ+Δℎ ,尽管也采用类似的 proj down → nonlinear → proj up 结构